The roots of Bayesian probability can be traced back to the 18th century, specifically to Thomas Bayes, an English statistician, philosopher, and Presbyterian minister.  Born around 1701 in London, Bayes made significant contributions to the field of probability and statistics. He was particularly influential in the development of what is now known as Bayesian inference. Bayes studied logic and theology at the University of Edinburgh before returning to England to work as a minister. His seminal work in probability, posthumously published in 1763, laid the groundwork for what Pierre-Simon Laplace would later expand upon, thereby solidifying Bayesian probability as a key concept in statistical analysis and machine learning, impacting how modern AI systems are developed and understood.
Born around 1701 in London, Bayes made significant contributions to the field of probability and statistics. He was particularly influential in the development of what is now known as Bayesian inference. Bayes studied logic and theology at the University of Edinburgh before returning to England to work as a minister. His seminal work in probability, posthumously published in 1763, laid the groundwork for what Pierre-Simon Laplace would later expand upon, thereby solidifying Bayesian probability as a key concept in statistical analysis and machine learning, impacting how modern AI systems are developed and understood.
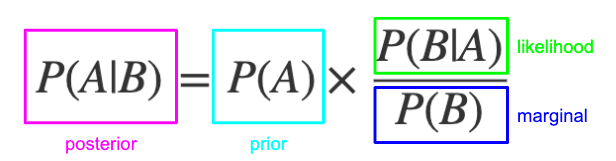
Bayesian Probability which in layman’s terms is “unending probability” or a way of predicting the likelihood of future events based on combining new evidence with prior beliefs or knowledge. This is a cornerstone concept in the field of AI and machine learning, and diverges fundamentally from the classical frequentist perspective. Unlike the traditional view of probability as a frequency or propensity measure, Bayesian probability is a representation of subjective belief or knowledge, encapsulating our understanding of uncertainties in events.